

Kate Berryman
cavaleri@uga.edu
*Please make sure your browser is maxiumized to view this write up;
Consider any triangle ABC. Select a point P inside the triangle and draw line AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. Prove Ceva's Theorem using ratios of AREAS.
Proof:
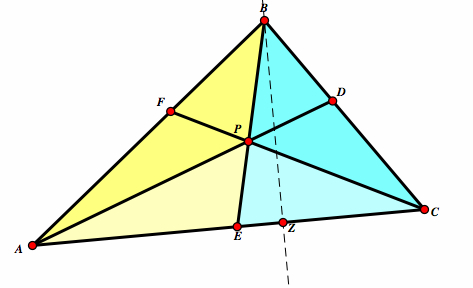
| Take △ABC. Select a point P inside the triangle and draw line AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. | 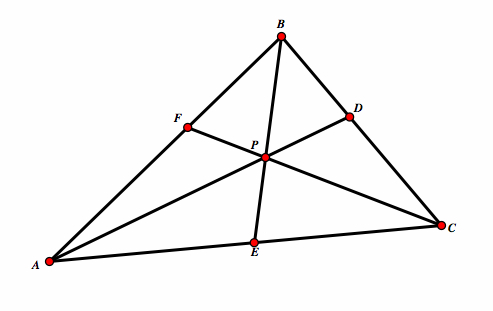 |
||||
| Construct a line passing through B and perpedicular to AC. Label this point X. | 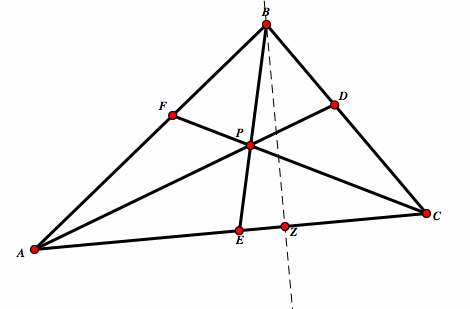 |
||||
Let's look at the area of two triangles. △ABE and △CBE both have the same height, BZ. △ABE has base AE and △CBE has base CE. Therefore: △ABE:△CBE = (AE/CE) |
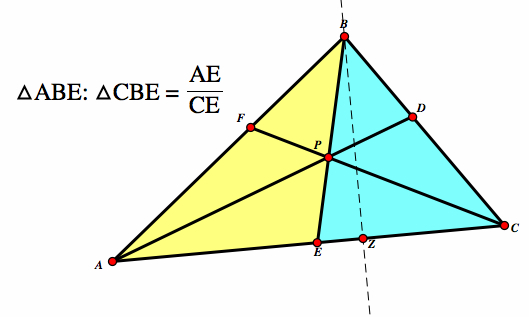 |
||||
Now, consider the smaller triangles △APE and △CPE. The same logic applies so therefore: △APE:△CPE = (AE/CE) |
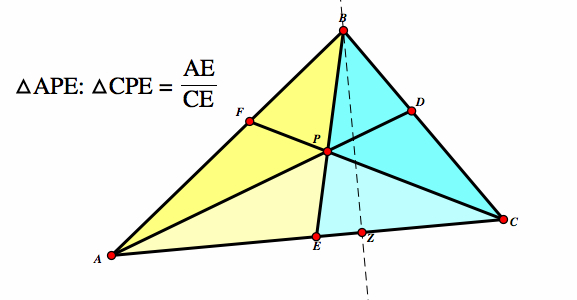 |
||||
If we look at △APB and △CPB and consider there areas we get: Area △APB = Area △ABE - Area △APE and Area △BPC = Area △CBE - Area △CPE |
 |
||||
We proved that:
It follows then by the same reasoning that the same is true for △CPA and △CPB and for the triangles △APB and △APC. Therefore:
|
|||||
Prove the converse of Ceva's Theorem.
Proof: We are given:
Take Take △ABC. Select a point P inside the triangle and draw line segments FP and DP.
If we can show that BPE are colinear, then we can show the converse of Ceva's Theorem. We know from Part 1 that :
If we mulitply these:
and simplify:
We were given:
So therefore:
Extend the segment BP until it meets the segment AC. Let's call this point Z. We just showed that:
We remember from part one that:
Therefore D=Z and our proof is complete. So when we extend our segment through P, it will intersect D. So we have proved the converse of Ceva's Theorem. Therefore, the medians of the triangles are concurrent.
|
Click Here to Return to Final Assignment Page
Click Here to Return to Kate's Homepage